Sudoku: von der Idee zum Endprodukt

Veröffentlicht am Freitag, 1. November 2024 | 15 min

In diesem Artikel möchte ich den Prozess des erstellen eines Sudokus veranschaulichen — von der Idee bis zum Endprodukt. Dabei geht es keineswegs um ein Standardverfahren oder ähnliches, es ist lediglich die Art und Weise, in der ich mich wohlfühle.

Achtung: Einige Inhalte dieses Artikels sind mathematisch etwas anspruchsvoll, aber ich gebe mein Bestes, das wichtigste zu erklären.

1. Schritt — Die Idee / Regel

Meine grobe Idee ist zunächst, ein Sudoku zu erstellen, das irgendein mathematisches Konzept braucht. Für dieses Projekt habe ich mich für Primzahlen entschieden. Ich führe folgende Regel ein:

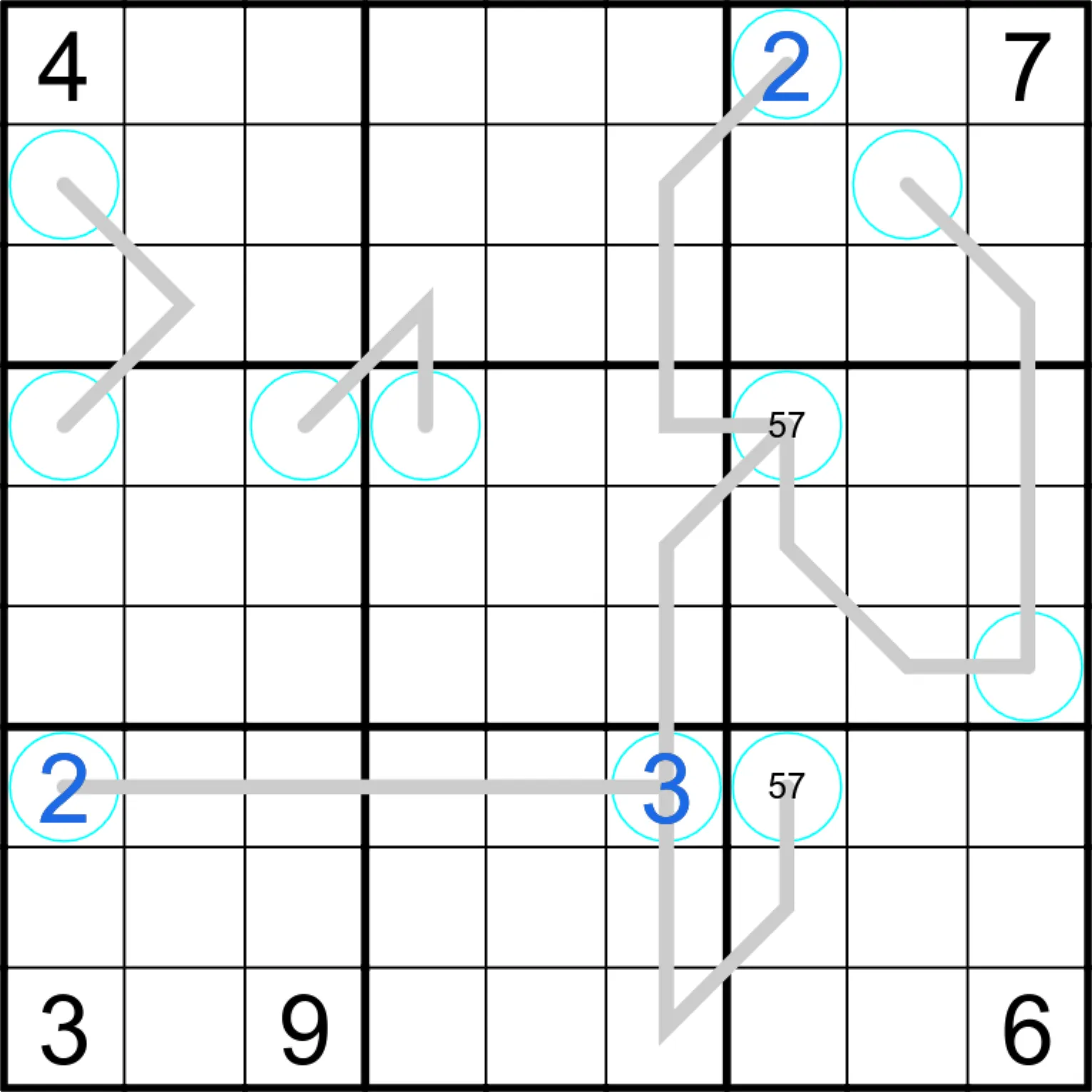
Ziffern in einem Kreis sind Primzahlen. Ziffern auf Linien zwischen zwei Kreisen haben (mindestens) einen der beiden Primzahlen in ihrer Primfaktorzerlegung

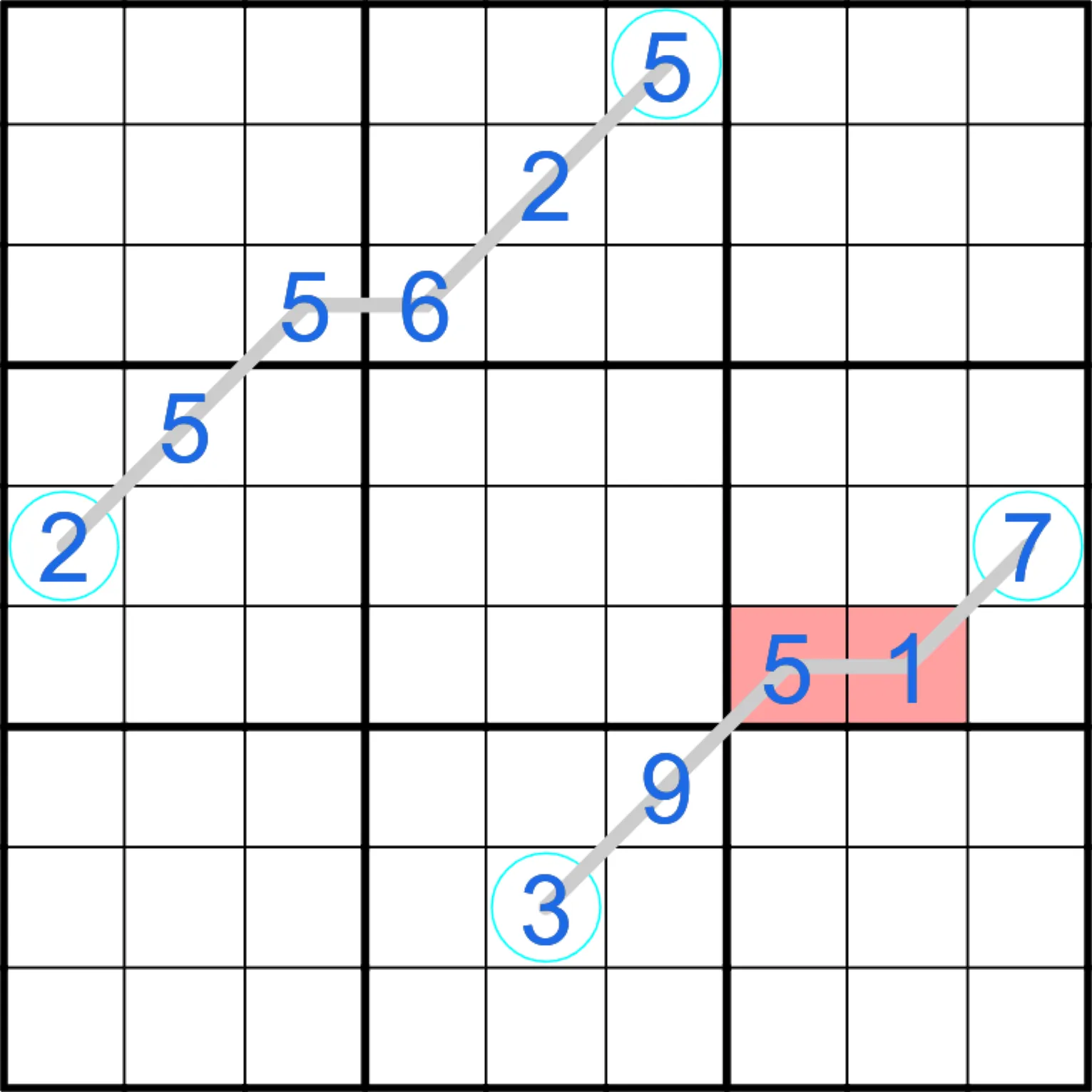
Um die Regeln etwas besser zu verstehen, hier erstmal ein Beispiel mit ein paar Kommentaren:

Ziffern können mehrmals auf einer Linie vorkommen, wenn dies die normalen Sudoku-Regeln zulassen
Die Primzahlen in den Kreisen selbst können ebenfalls auf der Linie sein
Die Ziffer 1 (in Rot) kann nicht auf der Linie sein, da sie in keiner Primfaktorzerlegung zu finden ist.
Die Ziffer 5 unten (in Rot) kann nicht auf der Linie sein, da sie weder Vielfaches von 3 noch von 7 ist.

Diese Regel lässt einiges an Flexibilität zu und gibt folgende Möglichkeiten, Einschränkungen zu setzen:

Einzelne Felder können auf die vier einstelligen Primzahlen (2, 3, 5, 7) beschränkt werden.
Die Ziffer 1 kann komplett von Kreisen und Linien ausgeschlossen werden.
Ist eine 5 oder 7 auf einer Linie, muss dieselbe Ziffer ebenfalls in einem Kreis sein.

2. Schritt — Ausprobieren mit der neuen Regel

Achtung!: Ab diesem Abschnitt gibt es Spoiler zum fertigen Sudoku. Wer das Sudoku zuerst selber probieren möchte, kann direkt zum Finalen Sudoku springen.

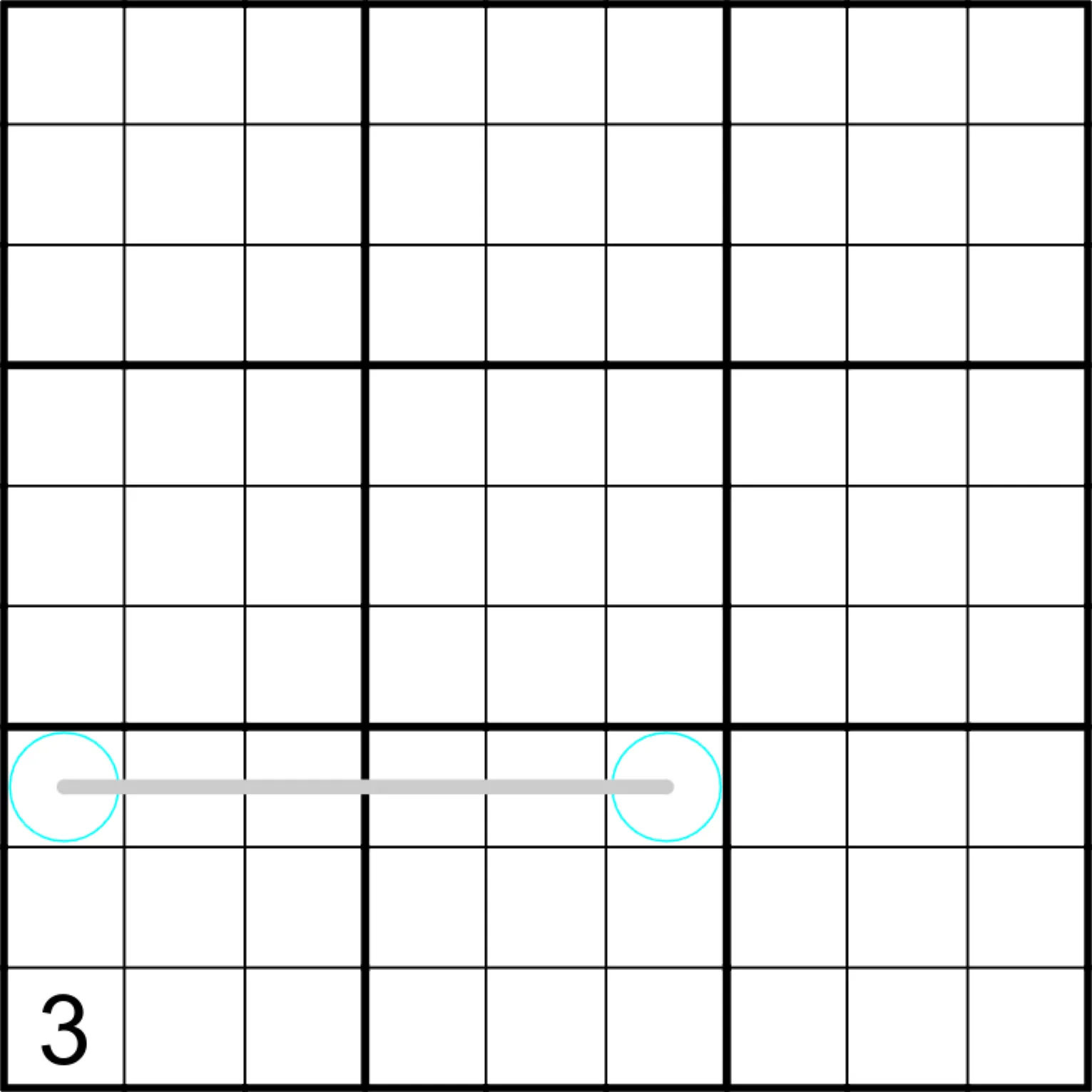
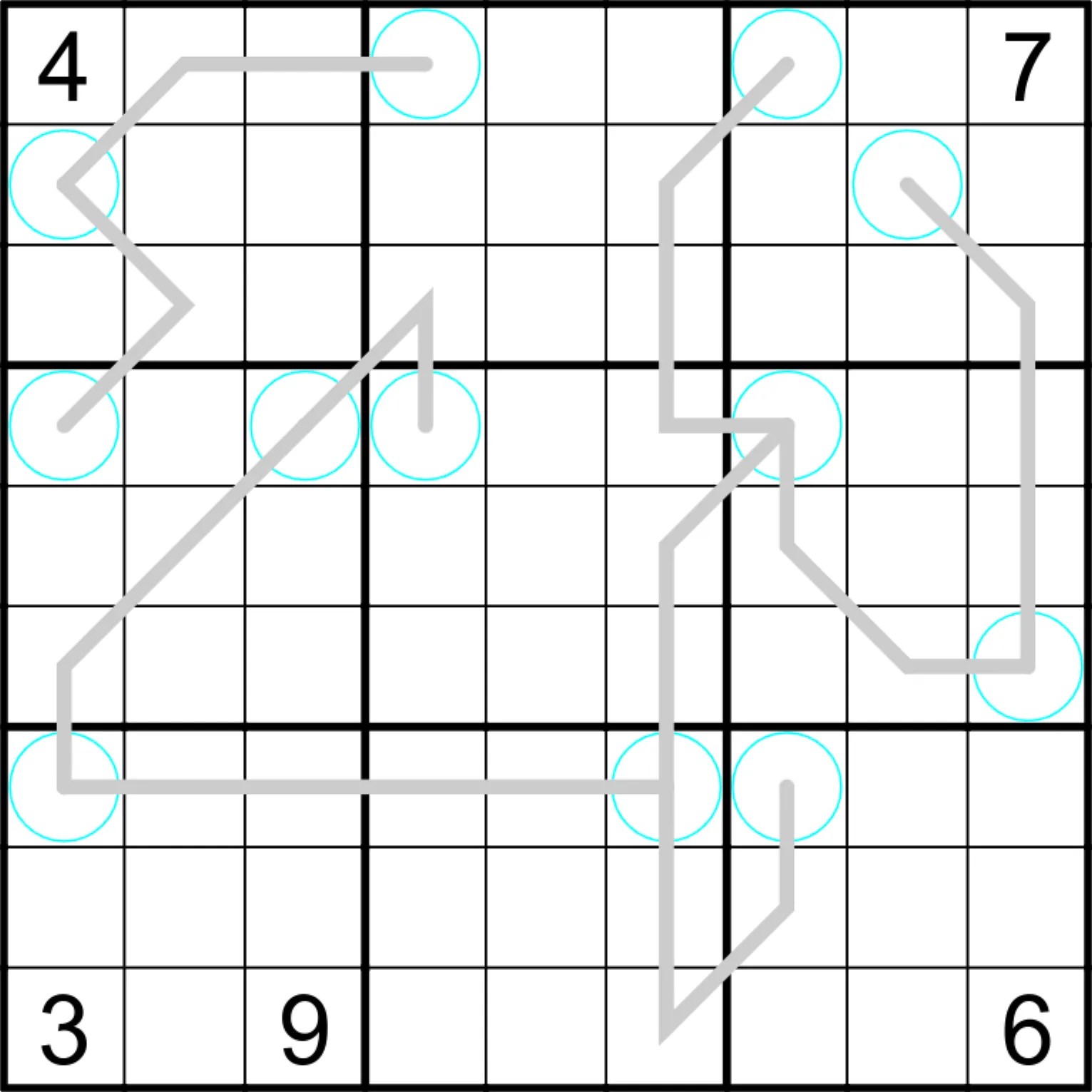
Wenn man eine neue Sudoku-Regel erfindet (oder entdeckt?, oder erschafft?), ist es wichtig, sich zuerst etwas damit auseinanderzusetzen, um zu verstehen, wie sie funktioniert. Meine erste Idee war die folgende:

Wie zuvor angesprochen, kann eine 1 weder in Kreisen, noch auf der Linie sein, deshalb muss die Ziffer 1 in der Zeile in die hintersten drei Felder.

Die Ziffern 5 und 7, die kein einstelliges Vielfaches besitzen können nicht auf die Linie, sonst müssten sie auch in den Kreisen sein, was die Sudoku-Regeln verletzt.

Ist eine 5 oder 7 in einem Kreis, müssen die Ziffern auf der Linie allesamt ein Vielfaches der anderen Ziffer auf dem Kreis sein. Da selbst die kleinste Primzahl 2 nur 3 einstellige Vielfache besitzt, ist es nicht möglich, die Linie zu füllen. Demnach sind 5 und 7 ebenfalls in den letzten drei Feldern.

In die beiden Kreise müssen nun die Ziffern 2 und 3, da alle anderen (ausser 1, 5 und 7) Vielfache von 2 oder 3 sind.

Dies soll auch der erste Schritt zur Lösung des Sudokus sein. Nun kommen wir zum nächsten, etwas komplizierteren Lösungs-Schritt, dem sogenannten Break-in.

3. Schritt — Das Break-in

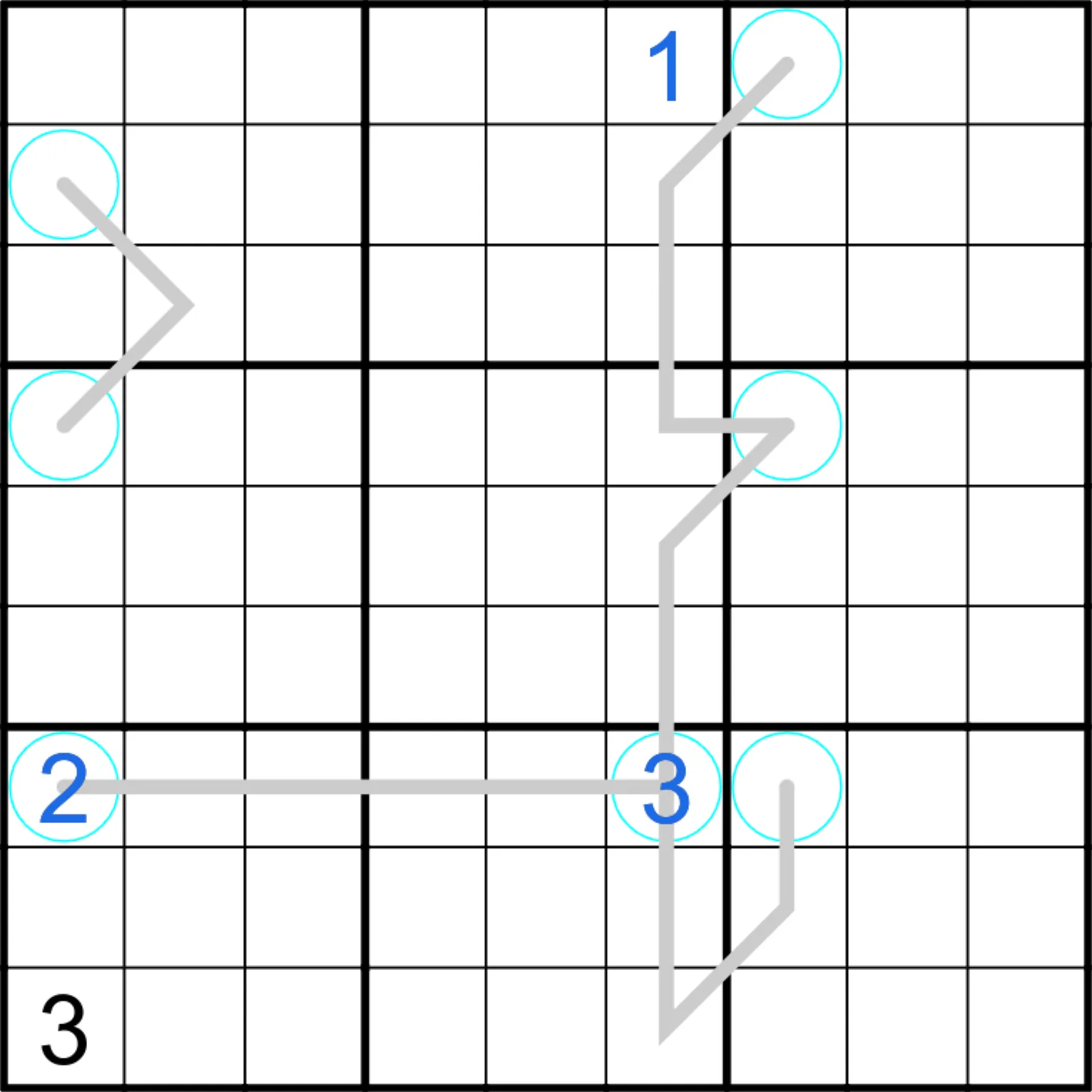
Das Break-in ist ein wichtiger Teil beim Lösen des Sudokus. Es bezeichnet einen etwas anspruchsvolleren Start in das Sudoku. Nach langem Ausprobieren, bin ich zu folgendem Break-in gelangt:

Im ersten Schritt wird der Fakt verwendet, dass die Ziffer 1 nicht auf Linien oder Kreise gesetzt werden darf. Demnach wird die 1 in Spalte 6 ganz oben platziert.

Der nächste wesentliche Schritt ist die Realisierung, dass die Ziffern 2, 5 und 7 auf den Linien in Spalte 6 ebenfalls in einem der Kreise in Spalte 7 auftauchen müssen.

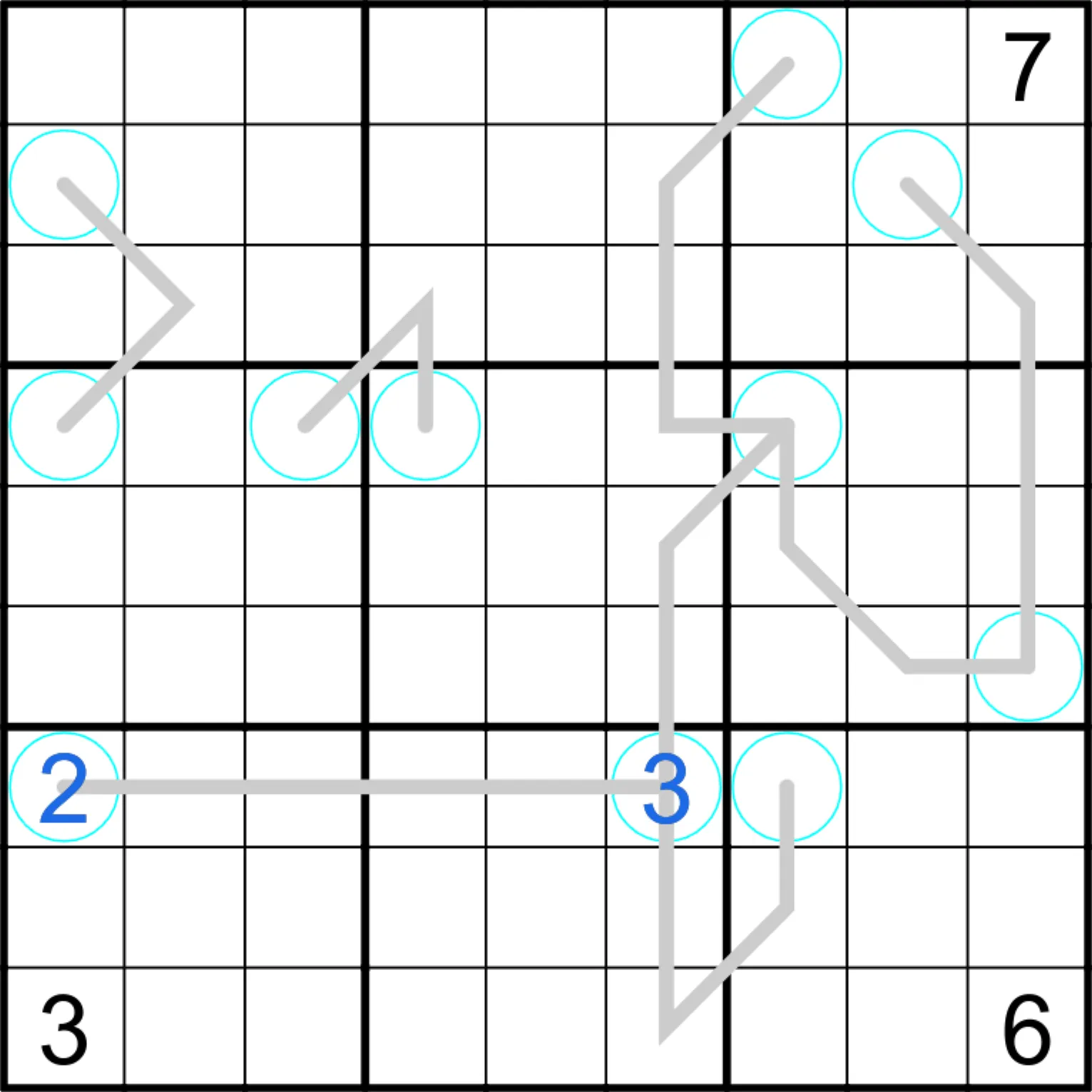
In einem weiteren Schritt füge ich weitere Einschränkungen hinzu, um die Ziffer 2 in Spalte 7 festzulegen:

Die wichtige Beobachtung hier ist der Kreis in Zeile 2 und Spalte 8. Befände sich in diesem eine 2, so wäre die Reihenfolge der Ziffern in den Kreisen in Spalte 7 von oben nach unten 5, 2, 7.

In dem Kreis in Spalte 9 müsste nun eine 3 stehen, denn sonst gibt es für auf die Linie keine drei Ziffern (ausser der 6), die ein Vielfaches von 2.

Nun müssten die Ziffern 5 und 7 in der mittleren Box in die mittlere Spalte (also Spalte 8). Da nun in Zeile 4 alle Primzahlen schon besetzt wären (vier Kreise), müssten 5 und 7 in die unteren zwei Felder in der Box. Dies würde zu einem Widerspruch auf der Linie führen, da diese nun eine 5 oder 7 enthielte, obwohl diese Ziffern kein Vielfaches der Ziffern in den Kreisen, 2 und 3, sind.

Demnach darf in die Ziffer im Kreis in Spalte 8 keine 2 sein und somit muss im Kreis in Spalte 9 eine 2 sein (für 3 und 5 gäbe es keine Ziffern, die auf die Linie passen würden). Die Ziffer 2 in jener Box zwingt die 2 in Spalte 7 in das Feld ganz oben in Zeile 1:

Letzter Schritt — Finales Sudoku

Ab diesem Zeitpunkt ist das Sudoku bereits ziemlich weit gelöst (theoretisch). Mit einigen weiteren Einschränkungen und vielem Ausprobieren komme ich schlussendlich zu dem finalen Sudoku:

Hierbei möchte ich mich noch herzlich bei David Clamage (Rangsk) bedanken, der viele Tools zum automatischen Lösen und Testen von Sudokus bereitstellt (Link zu seinem Sudoku-Solver)

Das finale Sudoku kann hier gespielt werden.

Konklusion

Das Erstellen eines Sudokus ist ein sehr Zeitaufwendiges Verfahren. Es hat mich einen halben Tag und viel Frust gekostet. Denn gerade der letzte Schritt beinhaltet viel ausprobieren in einem harten Kampf gegen den automatischen Sudoku-Solver.

Ich hoffe, ich konnte mit diesem Artikel den Prozess zum Erstellen eines Sudokus einigermassen gut aufzeigen. Viel Spass beim Lösen

Zurück